Entropy - Physics 298

In the Carnot cycle, shown above, we found that

But, Q_C represents heat leaving, which we have previously defined as negative. Therefore, if we define all Q's as heat entering (positive), we can write

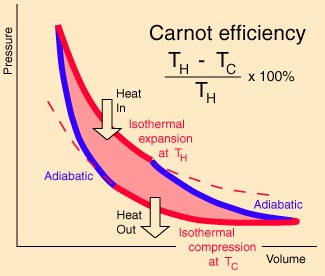
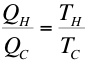
The above expression applies specifically to the Carnot cycle. It can be shown that any reversible cycle can be described as a sequence of infinitesimal Carnot cycles (see figure at right). In this case the summation above becomes an integral

where the circle on the integral tells us that the integral is evaluated over a complete cycle.

ENTROPY is defined by,

so that for a reversible cyclic process

Since entropy is unchanged in a complete cycle it is a "state" variable. Other state variables we have encountered include: pressure, temperature, volume, internal energy, gravitational potential energy. All these variables have specific values in one configuration of a system which are retained if the system leaves then returns to its initial configuration.

W and Q are NOT state variables. As we can clearly see in the Carnot cycle, there is net work done (area enclosed) and net heat entering (or leaving).

If the system in question does not undergo a complete cycle then

The change in entropy is independent of the path taken between initial and final states.

But all of the above analysis applies to reversible proceses. However, in nature there are no truly reversible processes ! So what use is this analysis ? The critical point is emphasized above, is independent of the path. Therefore, whether the path is reversible or irreversible the entropy change will be the same and we can use the above equation to calculate these entropy changes.

Using the above equation we can, in principle, calculate the entropy change for any process. In all cases we find that the total entropy of the system and environment increases. In fact the Second Law of Thermodynamics may be written in terms of entropy,

"A process linking two equilibrium states will proceed in the direction in which the total entropy of the system and environment increases"

where the equals sign applies for reversible processes.

Notice that the statement above describes the entropy change of the system and environment. It is possible for the entropy of a system to decrease, but the entropy of the environment will increase by a larger amount so that the net entropy increases. Sometimes the second law is simply stated "The entropy of the Universe is always increasing".

The concept of entropy isn't limited to thermodynamic systems. In fact, via statistical mechanics, it can be shown that entropy is related to the disorder in a system. The second law then states that "All allowed processes take place such that the disorder of the Universe increases".

Even more general still, it appears that the "arrow of time", the fact that time always flows in one direction (past to future), is defined by the necessity of the entropy of the Universe to increase.