
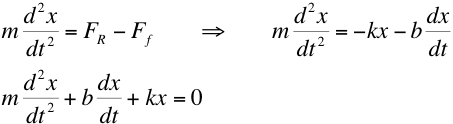
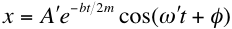
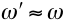 when the damping is small (small
b).
when the damping is small (small
b).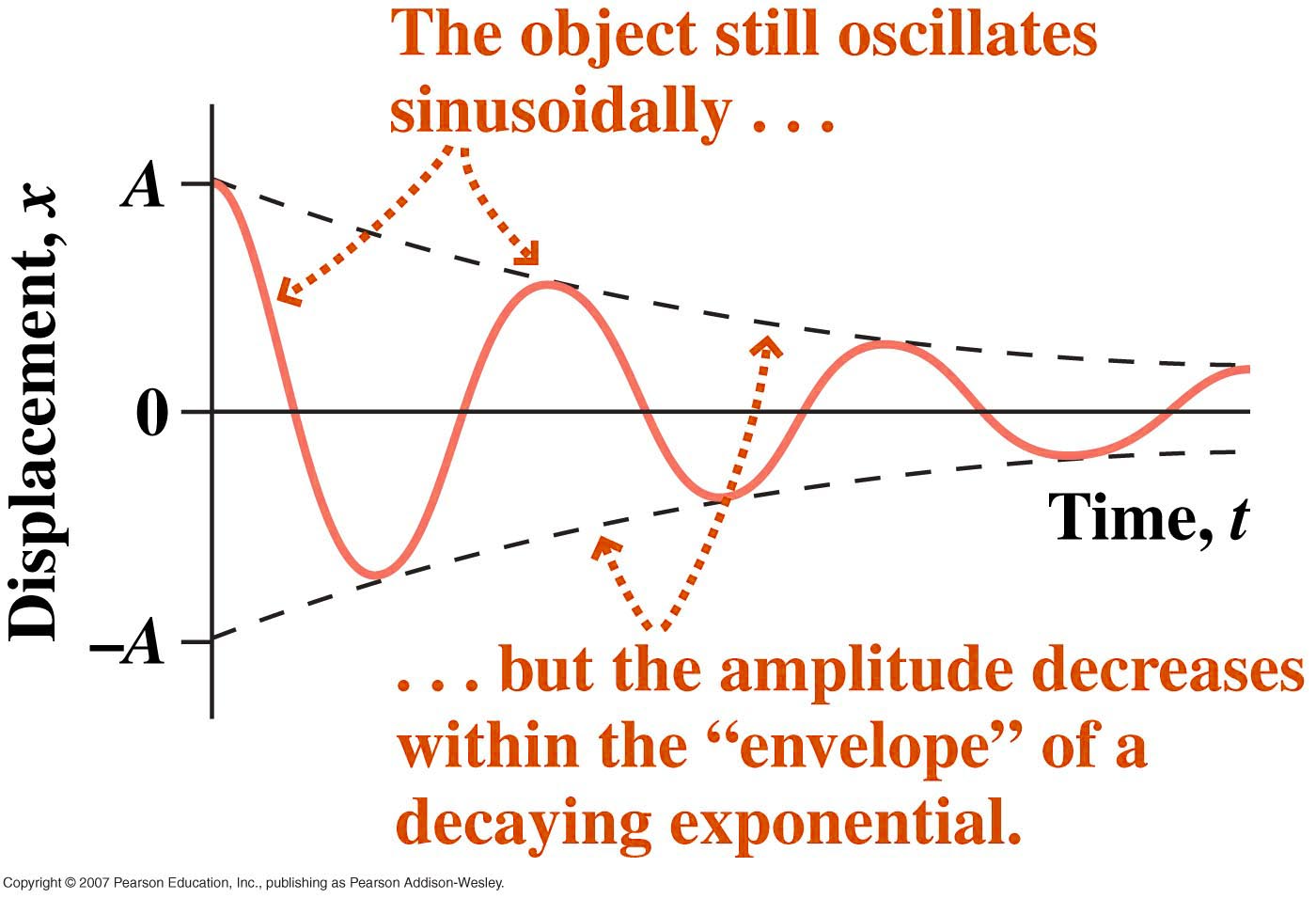
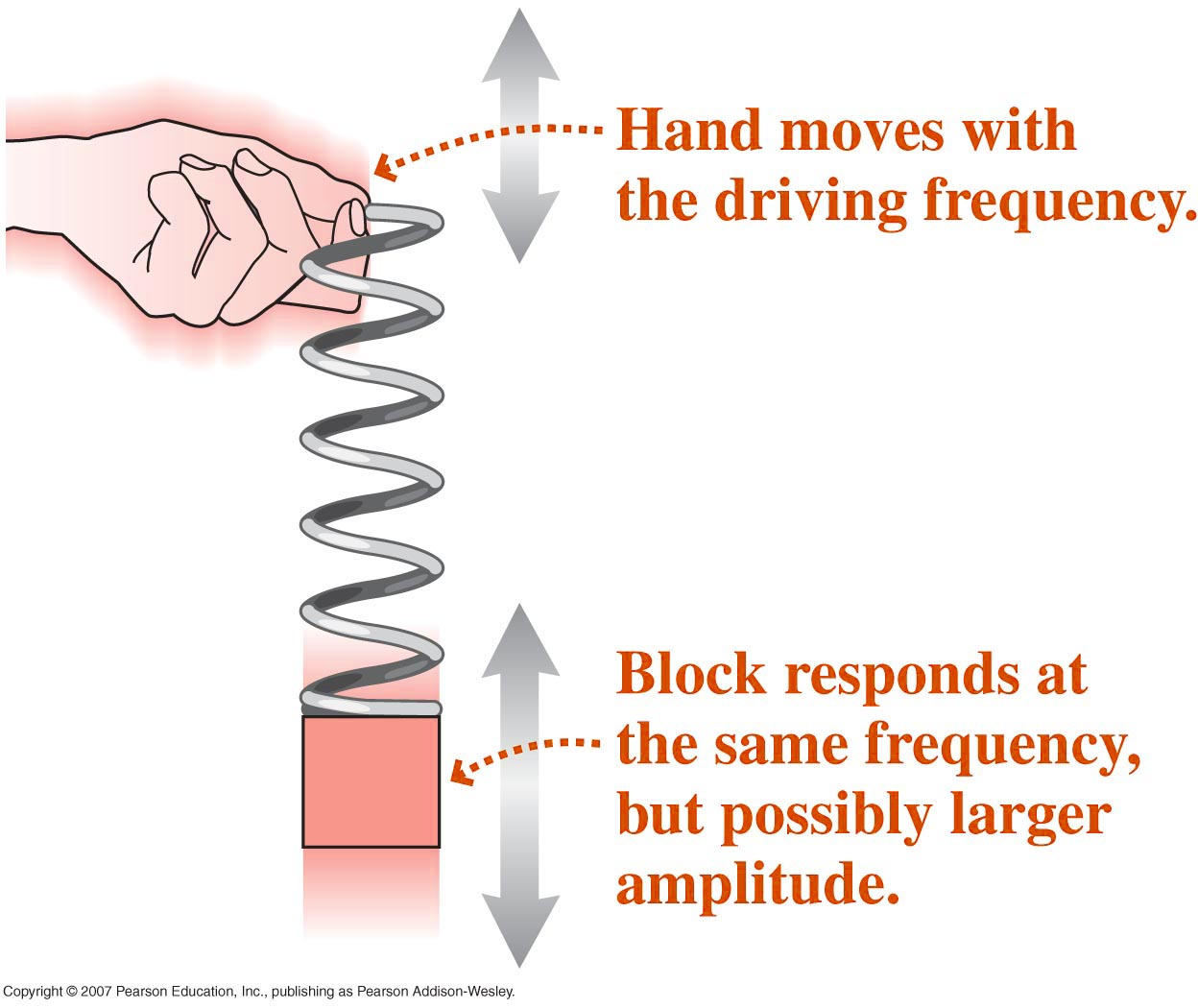 Suppose now
that instead of allowing our system to oscillate in
isolation we apply a "driving force". For
example, in the case of the (vertical) mass on a
spring the driving force might be applied by having an
external force (F) move the support of the spring up
and down. In this case the equation of motion of
the mass is given by,
Suppose now
that instead of allowing our system to oscillate in
isolation we apply a "driving force". For
example, in the case of the (vertical) mass on a
spring the driving force might be applied by having an
external force (F) move the support of the spring up
and down. In this case the equation of motion of
the mass is given by,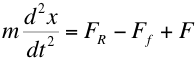
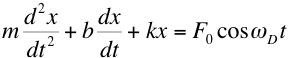
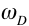 is the (angular) frequency
of the driving force.
is the (angular) frequency
of the driving force.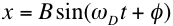
 where the
amplitude of these oscillations, B, depends on the
parameters of the motion,
where the
amplitude of these oscillations, B, depends on the
parameters of the motion, 
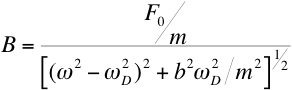
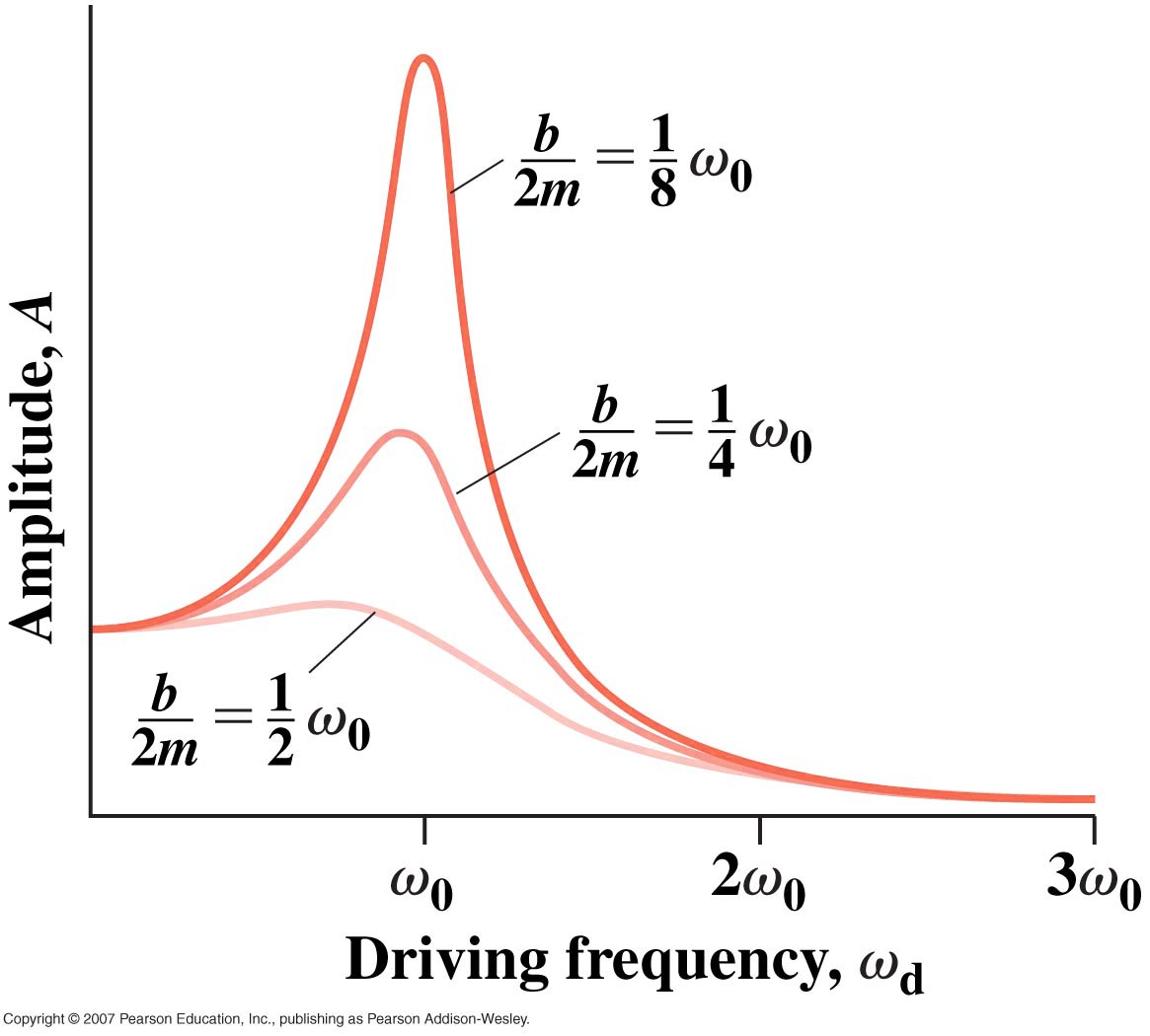
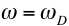 . This is called the resonance
condition. Note that at resonance, B, can become
extremely large if b is small. (In the diagram at
right
. This is called the resonance
condition. Note that at resonance, B, can become
extremely large if b is small. (In the diagram at
right 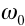 is the natural
frequency of the oscillations,
is the natural
frequency of the oscillations, 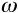 , in the
above analysis). In designing physical systems it is
very important to identify the system's natural
frequencies of vibration and provide sufficient damping
in case of resonance. This clearly did not happen
in the design of the Tacoma
Narrows Bridge (Tacoma
Narrows Newsreel) in 1940.
, in the
above analysis). In designing physical systems it is
very important to identify the system's natural
frequencies of vibration and provide sufficient damping
in case of resonance. This clearly did not happen
in the design of the Tacoma
Narrows Bridge (Tacoma
Narrows Newsreel) in 1940.
![]()
Dr. C. L. Davis
Physics Department
University of Louisville
email: c.l.davis@louisville.edu
