
 Magnetic
Monopoles
Magnetic
Monopoles 
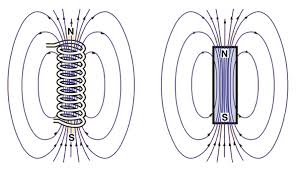



 Whereas with the
electric dipole it is possible to isolate the positive and
negative charges, experimentally it is not possible to
separate the North and South poles of a bar magnet.
Break a magnet in two and you get two magnets, each with a
North and South pole. Continuing this splitting
process down to the atomic level we find that even
elementary particles behave as magnetic dipoles, each with a
North and South pole. It appears that nature does not
allow us to create magnetic monopoles in this way.
Whereas with the
electric dipole it is possible to isolate the positive and
negative charges, experimentally it is not possible to
separate the North and South poles of a bar magnet.
Break a magnet in two and you get two magnets, each with a
North and South pole. Continuing this splitting
process down to the atomic level we find that even
elementary particles behave as magnetic dipoles, each with a
North and South pole. It appears that nature does not
allow us to create magnetic monopoles in this way.The belief is that shortly after their creation, magnetic monopoles were "frozen out" - meaning that their interactions with the rest of the matter in the Universe is highly suppressed. This does not prevent physicists from searching for evidence for the existence of magnetic monopoles.
Gauss' Law for Magnetism
Gauss' Law:
Ampere's Law:
Faraday's Law:
the flux of B through a closed surface is zero.
Note that the fact that the surface is closed is very important ! A magnetic flux integral appears in Faraday's Law - in this case the surface is generally not closed.
Electric field lines begin (positive) and end (negative) on charges. Since there are no magnetic charges magnetic field lines form closed loops.
A Princeton plasma physicist is at the beach when he discovers an ancient looking oil lantern sticking out of the sand. He rubs the sand off with a towel and a genie pops out. The genie offers to grant him one wish. The physicist retrieves a map of the world from his car an circles the Middle East and tells the genie, 'I wish you to bring peace in this region'.
Dr. C. L. Davis
Physics Department
University of Louisville
email: c.l.davis@louisville.edu
