

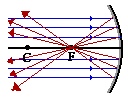
 The focal point (F) of a concave mirror is
the point at which a parallel beam of light is "focussed" after
reflection in the mirror. For a convex mirror the focal point is
the point from which light appears to have originated after reflection
from the mirror. The centre of curvature (C) is the centre of the
circle (sphere) of which the mirror is an arc.
The focal point (F) of a concave mirror is
the point at which a parallel beam of light is "focussed" after
reflection in the mirror. For a convex mirror the focal point is
the point from which light appears to have originated after reflection
from the mirror. The centre of curvature (C) is the centre of the
circle (sphere) of which the mirror is an arc.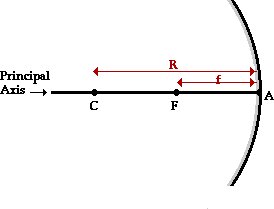 The focal length (f) and radius of curvature
(R) are defined in the diagram at the right. It can be shown that R =
2f. "A" in the diagram is known as the "vertex" (often
labeled V).
The focal length (f) and radius of curvature
(R) are defined in the diagram at the right. It can be shown that R =
2f. "A" in the diagram is known as the "vertex" (often
labeled V).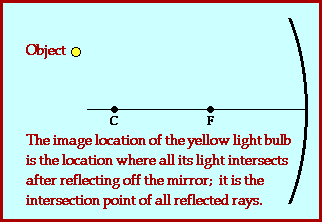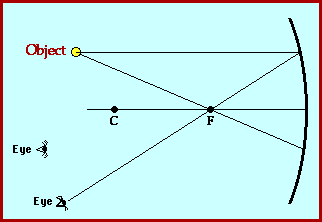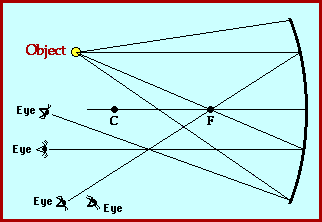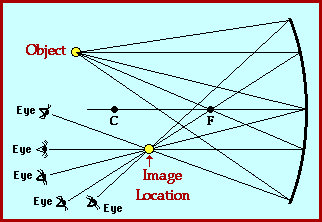
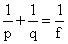
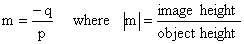
|
SIGN
|
+
|
-
|
|
f - focal length
|
Concave
|
Convex
|
|
p - object distance
|
Real
|
Virtual
|
|
q - image distance
|
Real
|
Virtual
|
|
m - magnification
|
Upright image
|
Inverted image
|
|
Mirror
|
Object location
|
Image location
|
Type
|
Orientation
|
Relative size
|
|
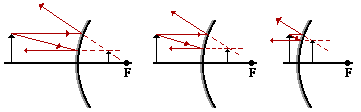
CONCAVE
|
At infinity
|
At F
|
Real
|
Inverted
|
Smaller
|
|
CONCAVE
|
Beyond C
|
Between F and C
|
Real
|
Inverted
|
Smaller
|
|
CONCAVE
|
At C
|
At C
|
Real
|
Inverted
|
Same size
|
|
CONCAVE
|
Between C and F
|
Beyond C
|
Real
|
Inverted
|
Larger
|
|
CONCAVE
|
At F
|
At infinity
|
No image
|
No image
|
No image
|
|
CONCAVE
|
Closer than F
|
Behind the mirror
|
Virtual
|
Upright
|
Larger
|
|
|
|||||
|
CONVEX
|
Anywhere
|
Behind the mirror
|
Virtual
|
Upright
|
Smaller
|
Dr. C. L. Davis
Physics Department
University of Louisville
email: c.l.davis@louisville.edu
