
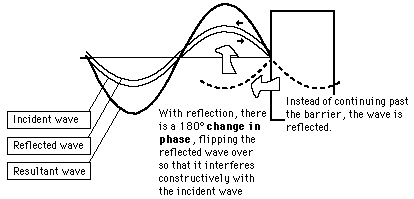
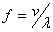 . The
wavelength (
. The
wavelength (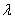 )
is given by 2L/n, where n can take on any positive integer value.
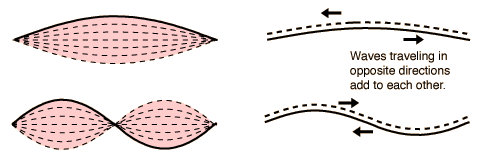
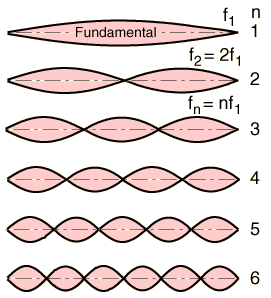
In the above diagram the upper standing wave has n=1 and the lower wave
has n=2.
)
is given by 2L/n, where n can take on any positive integer value.
In the above diagram the upper standing wave has n=1 and the lower wave
has n=2.
 The general expression for the frequency is given by
The general expression for the frequency is given by
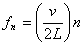 (n = 1,2,3,4....)
(n = 1,2,3,4....)
f1 is called the fundamental frequency or first harmonic.
f2 f3 f4 ... are called the 2nd, 3rd, 4th ... harmonics.
The standing wave patterns for n=1-6 are shown in the diagram at right.
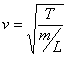
where T is the tension in the string and (m/L) is the mass per unit length of the string (kg/m). Tuning of a stringed instrument is achieved by adjusting the tension, which in turn changes the wave velocity and therefore the frequency.
 Supplementary Problems
Supplementary Problems
"Following the
dispute with the domestic servants' union at
Dr. C. L. Davis
Physics Department
University of Louisville
email: c.l.davis@louisville.edu
