Physics 111

Sample Test 1
Solutions

1) A driver sees a cow in the road ahead and applies the brakes so hard that they lock and the car skids to a stop in 15 m. The coefficient of kinetic friction between the tyres and the road is 0.75. Where necessary, assume g = 10 m/s².

(a) The shaded circle in the diagram below represents the car. Clearly indicate on the diagram the forces acting on the car as it brakes, labelling them appropriately. (This is known as a free-body diagram). (6)

(b) Write down the expression for the frictional force in terms of the normal force. This is the frictional force law. (3)

Kinetic friction:      F_f = µ _kN

(c) Which force causes the car to slow down and eventually stop ? Does the magnitude of this force change as the car slows down ? (2)

The frictional force causes the car to slow down and stop.

The magnitude of the frictional force is constant - independent of the velocity of the car.

(d) Use the value of the normal force and Newton's second law to determine the magnitude of the acceleration of the car. (6)

Newton's 2nd law along x axis
F = ma = F_f
therefore,     ma = µ _kN
but from Newton's 2nd law along the y axis,    N = mg
therefore,   ma = µ_kmg
and      a  =  µ _k g  =  0.75 x 10  =   7.5 m/s ²

(e) Use the appropriate equation describing one dimensional motion under constant acceleration to determine the initial speed of the car. (8)

a = -7.5 m/s²    ;    v_f = 0     ;     x = 15 m    ;     v _i = ?
Using,     x = (v_f² - v _i ² )/2a      with v _f = 0
then, v_i² = =2ax  =  -2 x (-7.5) x 15  =  15 x 15
so that,  v_i =   15 m/s

2) A force of 10 N pulls on an object located at the origin at an angle of 53^o with respect to the +y axis measured clockwise from this axis.

[cos 53 = 3/5 ; sin 53 = 4/5 ; tan 53 = 4/3 ]

(a) Indicate this force on the diagram below, labelling it F₁ . Make sure to also indicate the angle of 53^o on the diagram. (3)

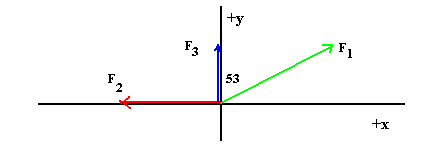
(b) Evaluate the x component of F₁ . (3)

F_1x = F ₁ sin53  =  10 x 4/5  =  8 N

(c) Evaluate the y component of F₁ . (3)

F_1y  =  F ₁ cos53  =  10 x 3/5  =  6 N

(d) A second force of 8 N acts on the object in the -x direction. Indicate this second force on the diagram as F₂. (2)

(e) Determine the x and y components of the total (resultant) force acting on the object. (5)

Define,       F₃ = F₁ + F₂
then,     F_3x = F_1x + F _2x      and   F_3y = F _1y + F _2y  
Using,   F_2x =  -8 N       and    F_2y = 0
then,     F_3x = 8 + (-8) = 0
and       F_3y = 6 + 0 = +6 N 

(g) Evaluate the magnitude of the resultant force. (3)

|F₃|  =  (F_3x²  +  F_3y² )^½   =   (0 + 36)^½
then,  |F₃|  =  6 N

3) A package is thrown vertically downward from a height of 3.2 m and hits the ground at 36 km/hr.

(a) Convert the speed with which the package hits the ground to m/s. (3)

v_f =   36 km/hr  =  (36 x 1000)/(60 x 60)  m/s  =  10 m/s

(b) Assuming the package moves under the influence of a constant gravitational acceleration of 10 m/s ² , what was the initial speed of the package ? (6)

v_f  =  -10 m/s   ;    y  =  -3.2 m    ;    a  =  -10 m/s²  
Using,      y  =   (v_f² - v _i ² )/2a
then,        v_i² = v _f ²  -  2ay  =  100  -  2 x (-10) x (-3.2)  =  36
therefore,     v_i  =   ± 6 m/s        [ choose -6m/s, v _i down ]

(c) How long does it take for the package to hit the ground ? (6)

Using,    a  =  (v_f  -  v _i)/t
then,       t  =  (v_f  -  v _i)/a  =  (-10  - (-6))/(-10)  =   0.4 s

(d) If the mass of the package is 2 kg, what is its weight ? (4)

Weight  =  mg  =  2 x 10  =   20 N

(e) If the mass of the package is 4 kg, which, if any, of your answers (b) and (b) would change?(2)

Parts (b) and (c) are independent of weight, therefore there are no changes.
(g is independent of the mass of the object)

(f) A second 2 kg package is thrown vertically upward from the same height and is observed to hit the ground at the same speed. What is the initial speed of this package ? (4)

  v_f  =  -10 m/s   ;    y  =  -3.2 m    ;    a  =  -10 m/s ²  
These are the same parameters as in part (b) above.  As in (b) we can solve for v_i giving v_i = ± 6 m/s
In this case we take the positive solution v _i =  + 6 m/s (upwards)

4) A skateboarder rolls from rest 6 m down the inclined plane shown below. The acceleration down the plane is observed to be 3 m/s².

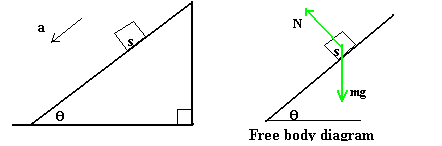
(a) Use the appropriate kinematic equation describing one dimensional motion under constant acceleration to determine how long it takes to cover the 6 m. (7)

a = 3 m/s²    ;     x  =  6 m     ;     v_i = 0     ;     t = ?
Using,     x = v_it + ½ at²
then with v_i = 0 we have,       x = ½ at ²
therefore,       t  =  (2x/a)^½   =  (2 x 6/3)^½  =   2 s

(b) Assuming the skateboarder rolls without friction, indicate on the free body diagram above all the forces acting on the person rolling down the slope. (6)

(c) Determine the component of the weight (w = mg) of the skateboarder along the slope in terms of w and . (6)

Along the slope the component of the weight = mg sin  =  w sin

(d) This component of the weight causes the observed acceleration. Use Newton's second law to obtain a value for sin or cos. (6)

[ Assume g = 10 m/s² ]

F  =  ma  =  w sin  =  mg sin
therefore,     a  =  g sin
so that,      sin  =  a/g  =  3/10  =  0.3