
Carnot's Theorem and Cycle

"Everyone has a right to a university
degree in America, even if it's in Hamburger Technology."
Clive James

- Having defined the efficiency and (coefficient of performance)
of a heat engine it can be shown that the second law places a
limit on the maximum attainable value of this efficiency.
This analysis can be split into two distinct parts - Carnot's
Theorem and the Carnot Cycle.
"The efficiency of all reversible
engines operating between the same two temperatures is the
same, and no irreversible engine operating between these
temperatures can have a greater efficiency than this"
- In order to understand this theorem we must first define what
we mean by a reversible and irreversible process. Without
a more detailed description of thermodynamics this is not an
easy task, however, the following statements give a flavor of
what reversibility involves,
- A reversible process is one
which can be made to "retrace" its path exactly.
- A process is reversible when the
successive states of the process are Infinitesimally close to
Equilibrium States. i.e. the process is quasi-equilibrium.
- With a reversible process it is
possible to restore the system to its original state without
needing an external agent or changing its surroundings.
- Reversible processes are an
abstraction that aids the analysis of real processes.
- A reversible process is a
standard of comparison for an actual system.
- Truly reversible thermal
processes would require an infinite amount of time for
completion.
All real physical proesses are
irreversible. Just as the ideal gas approximates the
behaviour of all gases, but no real gas is truly ideal; we can
devise processes which are close to being reversible, but never
quite get there.
The Carnot cycle is an ideal
reversible cyclic process involving the expansion and compression
of an ideal gas, which enables us to evaluate the efficiency of an
engine utilizing this cycle.
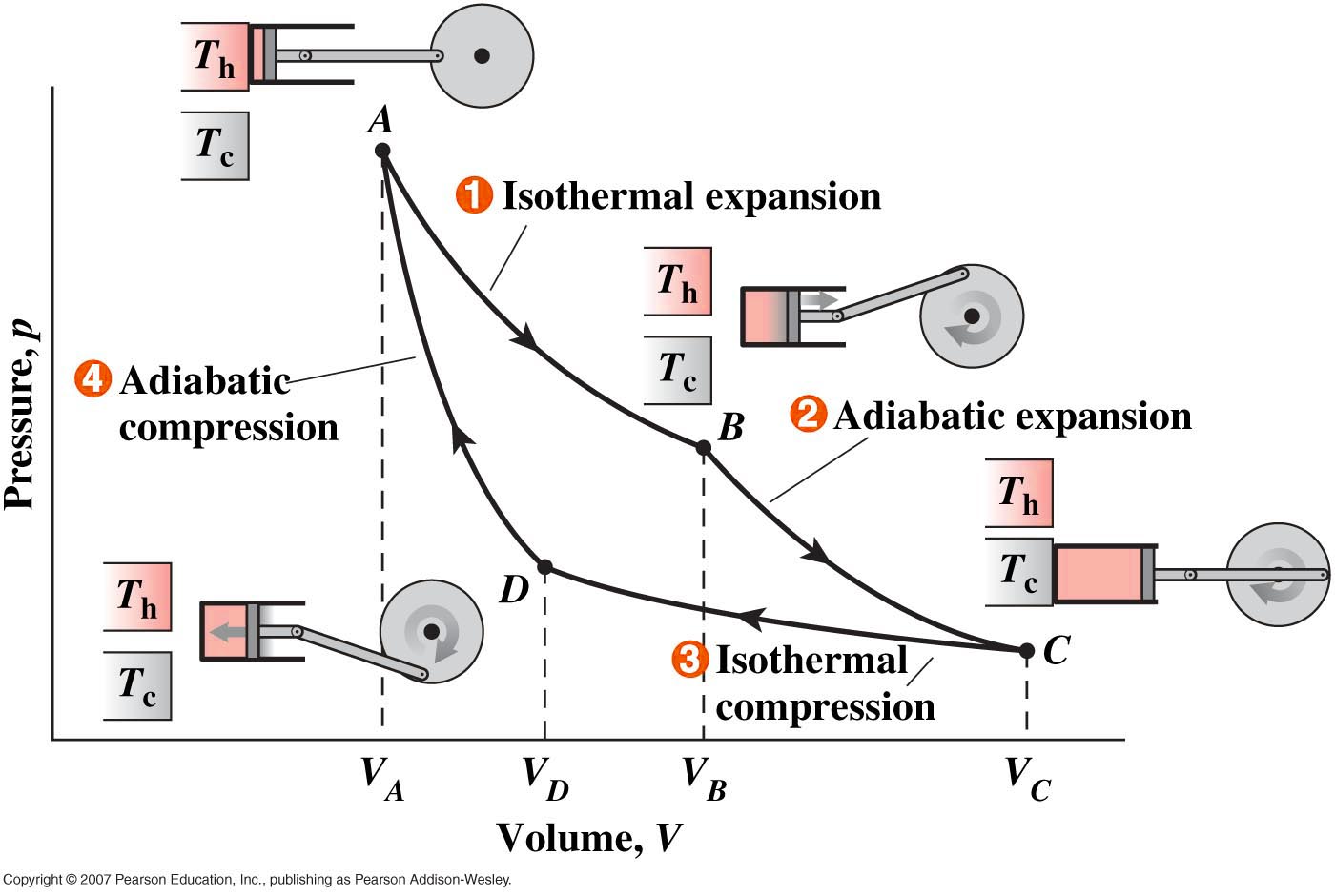
Each of the four distinct
processes are reversible. Using the fact that no heat
enters or leaves in adiabatic processes we can show that the
work done in one cycle, W = Q1 - Q3
where Q1 is the heat entering at tempertature TH
in the isothermal process A -> B and Q3 is
the heat leaving at temperature TC in the
isothermal process C -> D.
- By using the ideal gas equation (pV = nRT), the fact that
W = Q for isothermal processes and the fact that
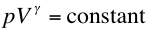 for adiabatic
ideal gas processes it can be shown that,
for adiabatic
ideal gas processes it can be shown that,
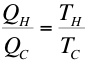
Therefore,
the efficiency of a Carnot cycle is given by,

Remember, this
is the
ideal heat
engine (reversible) efficiency. It sets
the maximum theoretically attainable efficiency of any
real engine
operating between the same two temperatures.

Be
careful. The temperatures in the ideal gas law
must be in Kelvin, therefore the temperatures in the
efficiency equation are also in Kelvin.

Q: What is
an astronomical unit?
A: One helluva big apartment

Dr. C. L. Davis
Physics Department
University of Louisville
email: c.l.davis@louisville.edu


 CARNOT'S
THEOREM
CARNOT'S
THEOREM
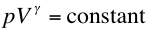 for adiabatic
ideal gas processes it can be shown that,
for adiabatic
ideal gas processes it can be shown that,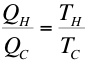
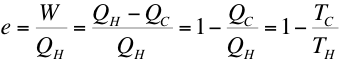
 Remember, this
is the ideal heat
engine (reversible) efficiency. It sets
the maximum theoretically attainable efficiency of any real engine
operating between the same two temperatures.
Remember, this
is the ideal heat
engine (reversible) efficiency. It sets
the maximum theoretically attainable efficiency of any real engine
operating between the same two temperatures.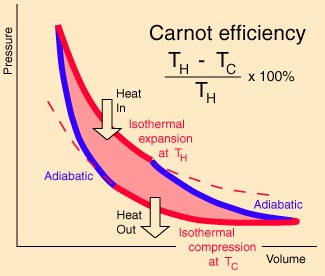
![]()
