A missile, mass (2/9) kg, is projected at an angle of 67 with the surface of the earth (assume horizontal), with a speed of 65 m/s.

    (a)   What is the horizontal component of the missile's velocity when it reaches its maximum
            height ? Ignore air resistance. (tan67 = 12/5)                                                          (3)

           Horizontal component is unaffected by the force of gravity, therefore,

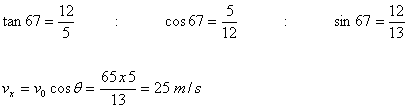
(b)   Use conservation of energy to determine the maximum height reached by the missile. Ignore
          air resistance. (g = 10 m/s²)                                                                                       (6)

where f is the top of the trajectory and I is the initial position.

           If we define U_g = 0 at ground level then,

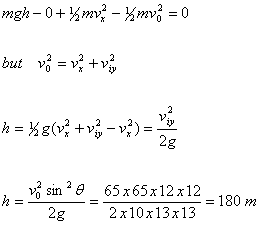
(c)   When it reaches its maximum height the missile explodes, breaking into two equal mass
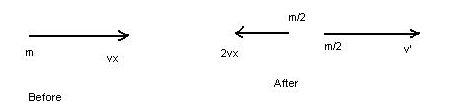
           fragments. One fragment is observed to move horizontally, to the left (see above), with a
           velocity equal to twice that of the horizontal component of the original missile immediately
           before the explosion. Determine the velocity of the other fragment immediately following
           the explosion.                                                                                                                  (8)

           Explosion is represented by the diagram below,

           Conservation of linear momentum during the explosion gives,

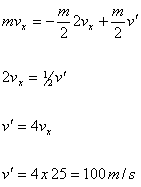
(d)   How much kinetic energy is lost (or gained) in the explosion ?                                   (6)

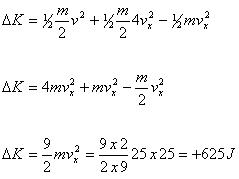
KE is gained

    (e)   Would you classify the explosion as elastic or inelastic ?                                         (2)

            Kinetic energy was not conserved which means the collision was INELASTIC