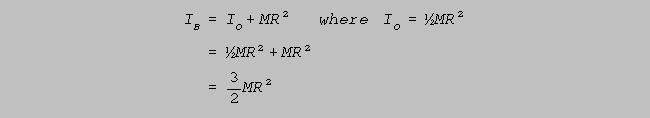
(b) A force of 30 N is applied at point A, as shown above. If the disc has a radius of 8 m,
determine the magnitude of the torque due to this force, abut the axis through B. (4)
The moment of inertia of a disc
about
an axis through its centre, perpendicular to its plane, is
given by MR,
where
R is the radius and M the mass.
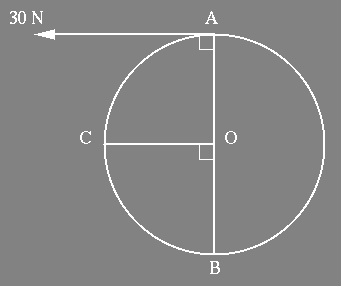
(a) Use the parallel axis theorem to obtain an
expression
for the moment of inertia of the disc,
about an
axis
perpendicular
to its plane, through its edge (at B).
(5)
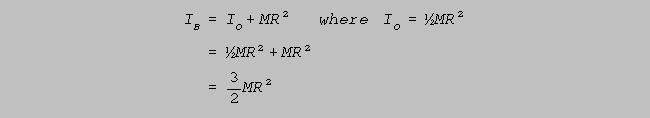
(b) A force of 30 N is applied at point A, as shown
above. If the disc has a radius of 8 m,
determine
the
magnitude
of the torque due to this force, abut the axis through B.
(4)
![]()
but r and
F are perpendicular in this case and r = 2R, therefore,
![]()
(c) What angular acceleration does this force impart
to the disc, when it rotates about the axis
through
B ?
(M = 2.5 kg)
(4)
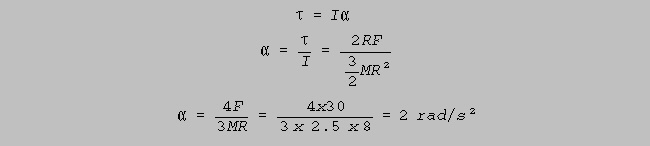
(d) The disk is rotating at 7 rev/min (about B),
when a mass of 2.5 kg is placed on its rim, at C.
What is the
angular
velocity (in rev/min) of the disc (and the mass), immediately
after the
mass is
positioned
on it ?
(8)
Conservation of angular momentum gives,
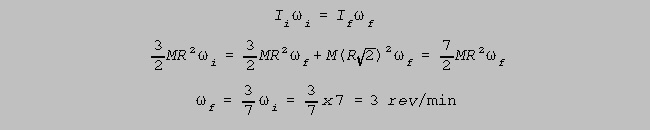
(e) What is the (linear) speed of the mass at this time ? (4)
