" You know, what Einstein has just said isn't so stupid"

Wolfgang Pauli

• We have seen that in a driven LCR circuit the current in the circuit oscillates with the driving frequency (that of the generator).  This current is an Alternating Current.  In real world applications many circuits will have a characteristic inductance (L), resistance (R) and capacitance (C) so that when provided with an alternating generator source of current/voltage the current in the circuit will be described by the solution to the differential equation in the driven LCR section.

• Rather than dealing with differential equation solutions engineers (?) came up with an alternative way of analyzing these ac circuits, by means of rotating vectors called phasors. 
  

• A phasor is a vector which rotates anticlockwise around the origin with the frequency of the generator, whose magnitude is the maximum value of a current or voltage.  The projection on the y-axis represents the instantaneous value of current or voltage.

R, C and L Phasors

• The current and voltage across each of the elements, R, C and L in a circuit can be represented by specific phasors.

•  Resistance

In a circuit with only the ac generator providing a voltage,  V(t) = V_Rm sinωt, and a resistance, R, the voltage and current across the resistor are given by,

  Note that the current and voltage phasors are in phase, as shown in the diagram at right. 

Note that in all phasor diagrams the magnitude of the phasors is the maximum value of the current or voltage, referred to as V_Rm and I_Rm .

• Capacitance

With the generator and a capacitance, we have,

where  is called the capacitive reactance.
Note that in this case the current phasor leads the voltage phasor by 90⁰.

• Inductance

With the generator and inductance alone, we have,

where    is called the inductive reactance.
Note that in this case the current phasor lags the voltage phasor by 90⁰.

Series LCR Circuits

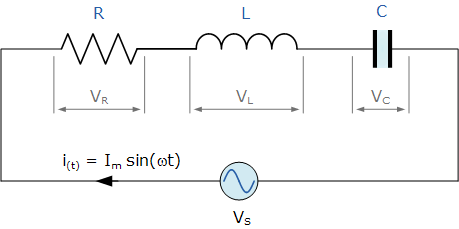• Combining these three elements - resistance, capacitance and inductance - in a series (LCR) circuit we may write

Now, treating these potentials as vectors (phasors), using the combined phasor diagram below we have

where i_m is the maximum current provided by the generator and Z is called the impedance, which plays a similar role to resistance in d.c. circuits.  In terms of the resistance, capacitance and inductance the impedance can be written,

• Notice that in the phasor diagram above the overall voltage phasor leads the current phasor by the angle θ, called the phase constant.   That is we can write  for the voltage as a function of time.  From the phasor diagram,

•   When V_L > V_C  the circuit is more inductive than capacitative.  In this case  X_L > X_C  and tanθ > 0.  X_C > X_L  and tanθ < 0 for more capacitative circuits.

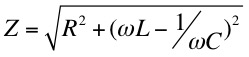
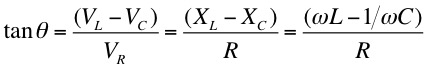
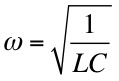• At resonance, when   ,  X_C = X_L so that tanθ = 0 (θ = 0) and  Z = R.  That is, the circuit is purely resistive with the current and voltage in phase.

Power Dissipation

• In an LCR circuit the energy supplied by the ac generator is either,
• stored in the magnetic field of the inductance,
• stored in the electric field of the capacitance or
• dissipated as thermal energy in the resistance.

As we have seen in the simple LC circuit the inductance (L) and capacitance (C) do not dissipate energy.  The energy simply oscillates from magnetic to electric without limit.  So in an LCR circuit energy can only be dissipated (lost) in the resistance (R).  The power dissipated is given by,

• The time-averaged power dissipation P_av is given by,

where is the "root-mean-square" of the maximum current.
Note that if we use the rms value of the current the expression for power dissipation in ac applications is the same as the "standard" expression used for dc applications.

AC current and voltage measuring devices are usually calibrated to read rms values.  In fact the 110 volts in a wall outlet is actually the rms value.  The maximum voltage is given by 110 x √2 = 170 V.

• In the LCR series circuit we have seen that  V_max = i_maxZ so that  V_rms = i_rmsZ.  Therefore,

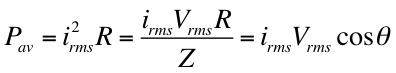
where from the LCR phasor diagram we see that cosθ = R/Z.

• Cosθ is called the Power Factor of the circuit. 
  

Maximum power dissipation occurs when cosθ = 1  or R = Z - the circuit is purely resistive.

• There are two ways to make an LCR circuit purely resistive
• Ensure resonance, X_C = X_L  or
• make (X_C - X_L ) as small as possible - that is, small L and large C.
  

Famous Physicists at a party : Volt thought the social had a lot of potential.

 
 

Dr. C. L. Davis
Physics Department
University of Louisville
email: c.l.davis@louisville.edu