" There is no democracy in physics. We can’t say that some second-rate guy has as much right to opinion as Fermi."

Louis Alvarez

• Having obtained the final form of Maxwell's equations we now consider several specific applications - LC oscillations, LCR circuits and ac circuits.

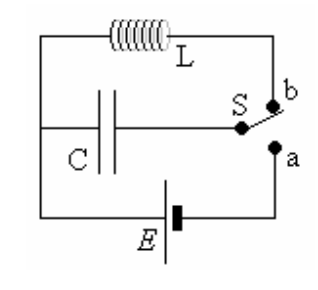
• Imagine a simple circuit which contains an (ideal) inductance, a capacitor and a source of emf which can be switched into or out of the circuit.

First we charge the capacitor by moving the switch to connect a and b.  On switching the switch to exclude the battery, now consider the LC circuit.  Applying the loop theorem we obtain,

 

but i = -dq/dt, since the charge on the capacitor is decreasing.  Therefore,

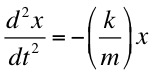•   Note that this equation is the same differential equation describing Simple Harmonic Motion     with m the particle mass, k the spring constant and x the displacement.  In fact there is a one-to-one correspondence between the behavior of electromagnetic oscillations in circuits and mechanical oscillating systems.

• One way to write the "general" solution to this differential equation is

where q_m and φ are constants determined by the "initial" conditions of the system. 
Substituting this general solution back into the original differential equation gives,

• Note that this solution describes the charge on the capacitor, q(t), which oscillates with angular frequency, ω.  The frequency is given by f = ω/2π.  The current through the inductance is given by,

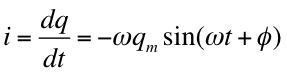
The capacitor is being charged and discharged as the current through the inductance reverses direction.

Energy Considerations

• The potential energy stored in the electric field of the capacitor is given by,

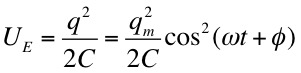
The potential energy stored in the magnetic field of the inductance is given by,

Therefore the sum of the electric and magnetic energy is

constant, independent of time, as shown below.

In the above graphs φ = 0

"Initial" Conditions

• As indicated above q_m and φ are determined by the "initial" conditions of the system.  For example, if when t = 0, q = q_max and i = 0 the system starts with a fully charged capacitor.  In this case at t = 0,

 

or φ  = 0, π, 2π, ...  Then

so that q_m = q_max.

• Alternatively, if at t = 0  q = 0 and i = i_max the capacitor is initially uncharged and the inductance has maximum current and we will find that φ = π/2, 3π/2, 5π/2 ....

Actually to determine q_m and φ we don't necessarily need the "initial" conditions, the values of q and i at any one value of t is sufficient.

Famous Physicists at a party : Coulomb got a real charge out of the whole thing.

 
 

Dr. C. L. Davis
Physics Department
University of Louisville
email: c.l.davis@louisville.edu