
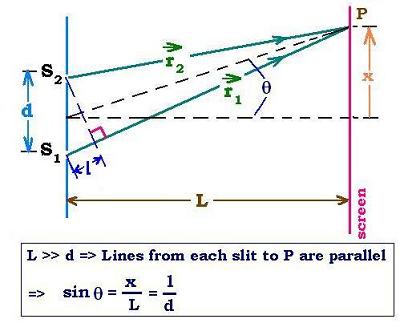

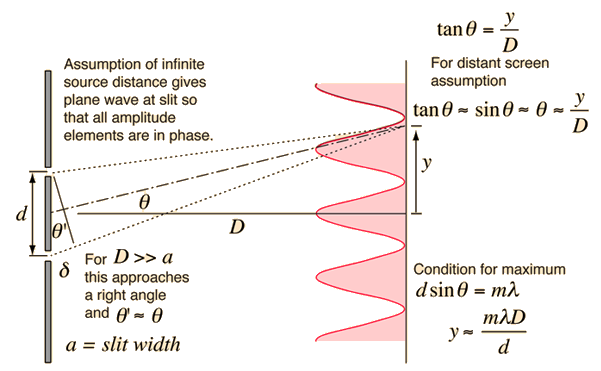

where n can take on integer values, n = 0, 1, 2, 3... and we have assumed that θ = θ' or in other words the separation of the slits is small compared to the distance to the screen (D >> d above).
Similarly, the condition for minimum intensity at P, when the path difference is a multiple of half wavelengths, is given by,
where n can again take on integer value, n = 0, 1, 2, 3...
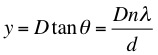
for the position on the screen for maximum intensity.
INTENSITY DISTRIBUTION in DOUBLE SLIT INTERFERENCE
 , the
experiment is still sometimes called Young's
slit experiment.
, the
experiment is still sometimes called Young's
slit experiment.In the above description we have assumed the incident light is monochromatic. If white light (containing all the wavelengths in the visible spectrum) is used, the maxima for the different wavelengths will occur at slightly different positions (y) on the screen. In this case an interference pattern will only be observed if the maximum - minimum separation is much larger than the separation between the maxima of the extreme wavelengths in white light (red and violet) for the same "n".
In the diagram at the top of this page the electric field from light originating at each of the slits S1 and S2 can be written,
where each slit has the same maximum E field, E0 and φ is the phase difference due to the path difference S1P - S2P.
Therefore the E field at P can be written,
the product of an amplitude and a sinusoidal time varying wave. In the case of light waves the frequency of the time varying part is so large that our eyes and most instruments "see" only the ampliutde part. Actually, what we observe is the intensity, which is the square of the amplitude. The intensity observed at P is then given by,
as shown in the red shading in the diagram above. Note that maxima of the above cosine squared function occur when φ = 2π n; this leads to bright spots on the screen.
Thus for small values of θ (sinθ = θ), φ and θ are proportional to each other.
COHERENCE
For long wave radiation (e.g. radio waves) a single source illuminating the two slits results in two coherent sources, since this type of radiation is typically produced in a continuous waveform, as shown at left below.
For short wavelength radiation (e.g. light) "waves" are typically emitted by multiple individual atoms in a random incoherent manner (no definite phase between these multiple "sources"). The radiation is emitted in "packets" rather than as a continuous wave. Thus a two slit configuration, at left below, will not produce an interference pattern. In order to observe an interference pattern with light the configuration at right below must be employed. The single slit to the left of the two slits ensures that light reaching the two slits is from the same part of the source and therefore in phase.
Note that a laser beam produces a coherent light source and can be used to create an interference pattern in the left configuration.
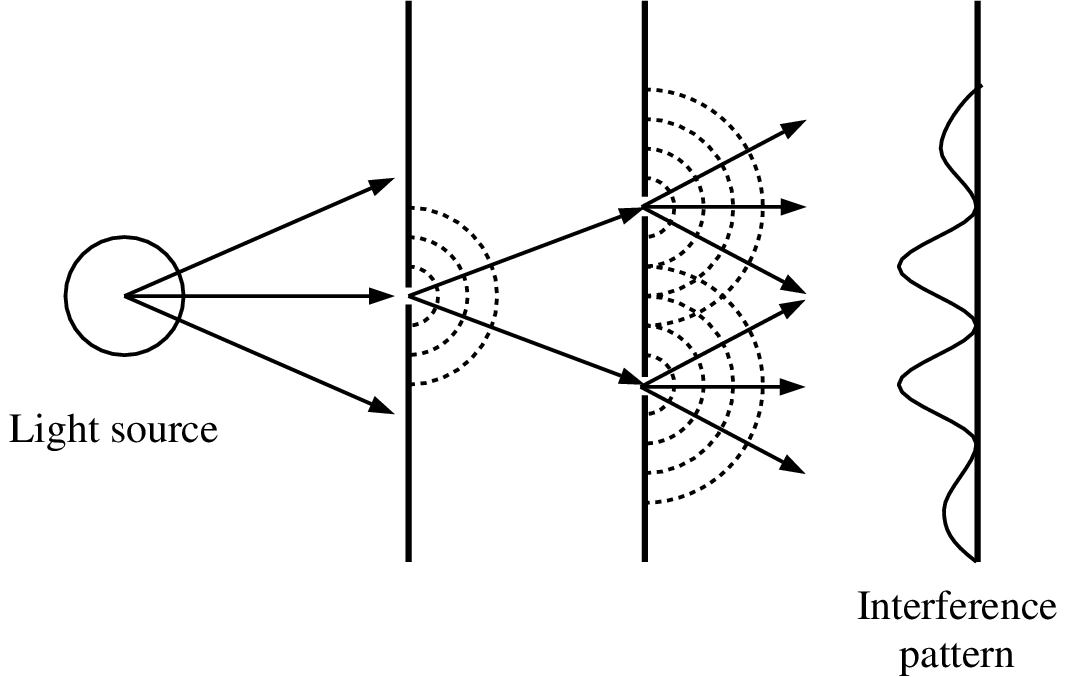

 Consider
double slit
interference. In the
figure at right there are
locations on the screen
which have zero light
intensity.
Consider
double slit
interference. In the
figure at right there are
locations on the screen
which have zero light
intensity.


Dr. C. L. Davis
Physics Department
University of Louisville
email: c.l.davis@louisville.edu
