
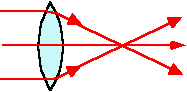
 Converging Lens.
Parallel light incident on one side of a converging lens
passes through a single point on the other side called the "focal
point" (F). This is achieved due to refraction at
both surfaces of the lens because light travels more slowly in
glass than air.
Converging Lens.
Parallel light incident on one side of a converging lens
passes through a single point on the other side called the "focal
point" (F). This is achieved due to refraction at
both surfaces of the lens because light travels more slowly in
glass than air.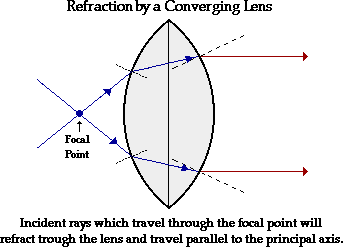
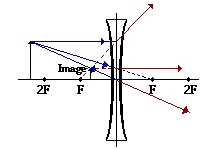
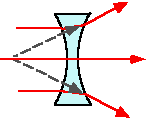 Diverging Lens.
Parallel light incident on one side of a diverging lens is
seen to diverge, as if the light came from a single point on the
same side of the lens as the incident light. This point is
known as a " virtual focal point", since after passage
through the lens, light does not pass through it. As in the case
of the converging lens light is refracted at both surfaces
passing more slowly through glass than air.
Diverging Lens.
Parallel light incident on one side of a diverging lens is
seen to diverge, as if the light came from a single point on the
same side of the lens as the incident light. This point is
known as a " virtual focal point", since after passage
through the lens, light does not pass through it. As in the case
of the converging lens light is refracted at both surfaces
passing more slowly through glass than air.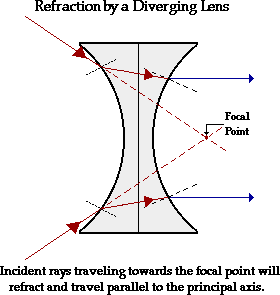
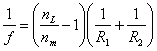
|
SIGN
|
+
|
-
|
|
Focal length - f
|
Converging Lens
|
Diverging Lens
|
|
Radii of curvature - R
|
Convex Surface
|
Concave Surface
|


|
SIGN
|
+
|
-
|
|
f - focal length
|
Converging lens
|
Diverging lens
|
|
p - object distance
|
Real
|
Virtual
|
|
q - image distance
|
Real
|
Virtual
|
|
m - magnification
|
Upright image
|
Inverted image
|
|
Lens
|
Object location
|
Image location
|
Type
|
Orientation
|
Relative size
|
Application
|
|
CONVERGING
|
Infinity
|
At F
|
Real
|
Inverted
|
Smaller
|
Telescope
|
|
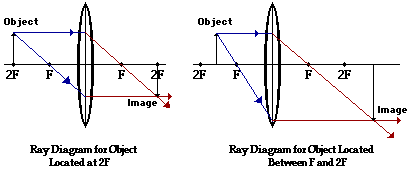
CONVERGING
|
Beyond 2F
|
Between F and 2F
|
Real
|
Inverted
|
Smaller
|
Camera
|
|
CONVERGING
|
At 2F
|
At 2F
|
Real
|
Inverted
|
Same size
|
Copier
|
|
CONVERGING
|
Between F and 2F
|
Beyond 2F
|
Real
|
Inverted
|
Larger
|
Projector
|
|
CONVERGING
|
At F
|
At infinity
|
No image
|
No image
|
No image
|
Lighthouse
|
|
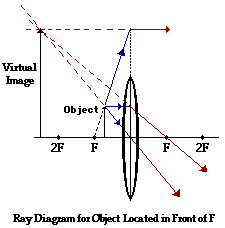
CONVERGING
|
Closer than F
|
Same side of lens
|
Virtual
|
Upright
|
Larger
|
Magnifying glass
|
|
|
||||||
|
DIVERGING
|
Anywhere
|
Same side of lens
|
Virtual
|
Upright
|
Smaller
|
|
Dr. C. L. Davis
Physics Department
University of Louisville
email: c.l.davis@louisville.edu
