Magnetism - Displacement Current

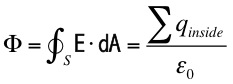
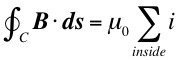
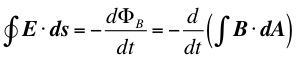
Faraday's Law: magfaradayeqn6

Nobody's Law:

Looking carefully at these equations, the two flux equations are now consistent with our physical understanding of electric and magnetic charges.

The line integrals are a different matter. The right hand side of Ampere's Law has a summation over electric currents. Naively we would expect a similar sum over "magnetic currents" on the right hand side of Faraday's Law. But since there are no magnetic charges, "magnetic currents" do not exist and the necessity for such an additional term disappears.

However, in words, Faraday's Law states that

"A changing magnetic field ( ) gives rise to an electric field ( )"

For a more complete correspondence between E and B we would expect a term added to the right hand side of Ampere's Law which indicates,

"A changing electric field ( ) gives rise to a magnetic field ( )"

Maxwell proposed this addition, the existence of which is now physically verified. Furthermore, Maxwell showed that this additional term, known as the displacement current, is essential for the description of electromagnetic waves.

divider

Inconsistency in Ampere's Law

Ampere's Law can be written

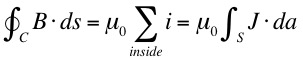
where we have made use of the general relationship between current and current density,

Note that the surface over which the flux of J is evaluated, S, can be any open surface bounded by the closed Amperian loop C.

In the figure at right, showing a schematic of a parallel plate capacitor being charged, 4 possible surfaces are shown bounded by a single Amperian loop. For each of these surfaces the flux of J must give the same current. As indicated, surfaces 1, 2 and 4 are "pierced" by the current I. However, as can be seen, no current passes through surface 3.

What to do about this inconsistency ?

Fixing Ampere's Law

The existence of a Displacement Current "flowing" between the plates of the capacitor, passing through surface 3, is the solution. The displacement current through surface 3 must be equal to the "normal" (conduction) current passing through surface 1.

The conduction current through surface 1 can be written,

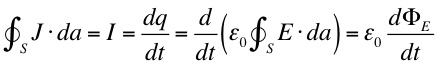
Therefore, if we define

as the displacement current, by writing

we can ensure this inconsistency in Ampere's Law is removed.

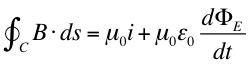
Therefore, including the displacement current, Ampere's Law becomes,

divider

Parallel Plate Capacitor

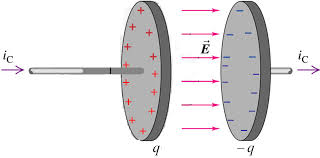For a parallel plate capacitor we have,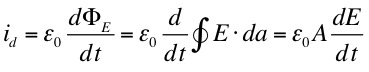

where,

therefore,

So that the displacement current i_d is equal to the conduction current bringing charge to the plates, i.

The displacement current can be considered to be distributed throughout the volume between the plates. The associated magnetic field can be calculated in a similar manner to that due to a thick wire carrying (conduction) current.

The direction of the magnetic field created by the displacement current can be found by applying the right-hand rule in the usual way - thumb points in the direction of the (displacement) current, fingers wrap around in the direction of the magnetic field. The direction of the displacement current itself is in the same direction as E if E is increasing with time (dE/dt > 0). When E is decreasing with time the displacement current is opposite to E (dE/dt < 0).

So why didn't Faraday and others detect the displacement current

The presence of the displacement current would be signaled by detection of its associated magnetic field. Assuming only a displacement current we can write Ampere's Law,

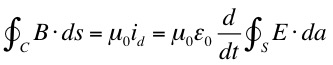
magdisplacementeqn13

so that,

where A is a representative cross section and l a representative length.

Thus, unless dE/dt and A/l are very large, B will be very small. In Faraday's time it was technologically impossible to vary the E field fast enough to obtain a measurable B.