
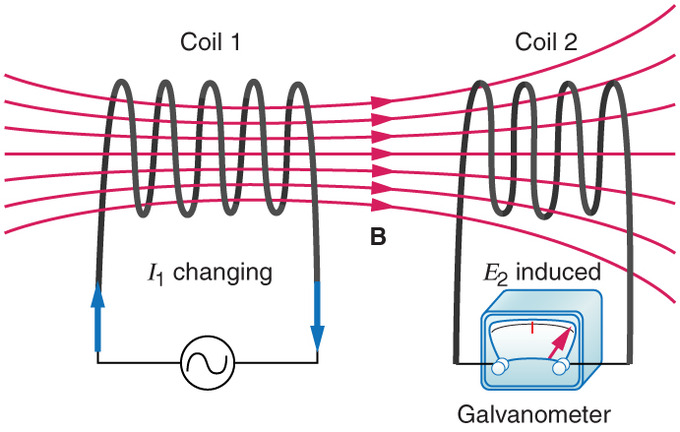
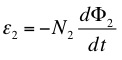
but the total flux through circuit 2 is proportional to the current in circuit 1, where the proportionality constant is called the mutual inductance of the coils, M21,
Combining these two equations gives
In other words the emf in circuit 2 is proportional to the rate of change of current in circuit 1. As we will see shortly, the mutual inductance M21 depends only on the geometric configuration of the two circuits.


The concept of inductance is related to the magnetic field in a similar way that capacitance is related to the electric field.
You will always find that M depends only on the geometric parameters of the two circuits and the number of turns in each circuit.
- Determine B due to one circuit at the location of the other using Ampere's Law or the Biot-Savart Law.
- Using this B calculate the magnetic flux through the 'other' circuit.
- Then use the equation N2Φ2 = MI1 to obtain M.
This girl said she recognized me from the vegetarian club, but I'd never met herbivore.
Dr. C. L. Davis
Physics Department
University of Louisville
email: c.l.davis@louisville.edu
