
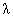 . The
wavelength of a
particle, called the
deBroglie
. The
wavelength of a
particle, called the
deBroglie wavelength, is given by
wavelength, is given by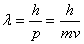
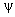 .
. 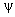 itself
has no physical meaning, but
itself
has no physical meaning, but 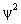 is
proportional
to the probability of finding the particle
at a particular point in space.
is
proportional
to the probability of finding the particle
at a particular point in space. Supplementary Problems
Supplementary Problems
Dr. C. L. Davis
Physics Department
University of Louisville
email: c.l.davis@louisville.edu
