Physics 298
Sample Test 1
1. (a) a is a unit
vector in the yz plane, having a negative z
component. The y component of a is
0.8.
Evaluate the z component of a. (3)
(b) Write a in the i, j, k format (2)
(c) What is the tangent of the angle between a and the +z axis ? (3)
(d) b is also a unit vector. Its y and z components are (3/7) and (-3/7), respectively.
Calculate the x component of b. (4)
(e) Use the dot product to evaluate the cosine of the angle between a and b. (6)
(f) What is the magnitude of the vector given by a x b ? (7)
2. A
large boulder is ejected vertically upward from a volcano with an initial speed
of 100 m/s. Air resistance may be
ignored. [g = 10 m/s2
]
a. At what time after being ejected is the boulder moving at 30 m/s upward ? (5)
b. At what time is it moving at 30 m/s downward ? (5)
c. When is the displacement of the boulder from its initial position zero ? (5)
d. When is the velocity of the boulder zero ? (5)
e. What are the magnitude and direction of the acceleration while the boulder is moving (i) upward ? (ii) downward ? (iii) at the highest point ? (2)
f. Sketch ay , vy and y versus t on the diagrams below (assume that y = 0 at the moment the boulder is ejected). (3)
3). A
ball moves at a constant speed of 2 m/s on a horizontal plane following the
path AOBCDEOF, where BCDE is a circular arc. The radius of the circular part of the path is 4 m.
Use the gross approximation pi = 3 throughout this problem.
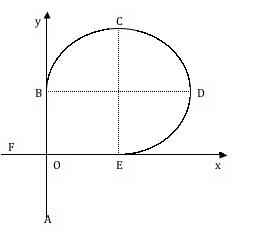
(a) Calculate the distance
traveled by the ball along the round trip OBCDEO. (2)
(b) How long does it take the ball
to complete this round trip ? (3)
(c) Evaluate the magnitude
of the instantaneous acceleration felt by the ball at C. On the diagram, clearly indicate the
direction of the instantaneous acceleration at C. (5)
(d) Write the instantaneous
velocity at B in unit vector form. (2)
(e) Obtain the average
acceleration vector in unit vector form between points B and D. (5)
(f) Obtain the average
velocity vector in unit vector form between B and E. (5)
(g) Calculate the average
velocity over the round trip OBCDEO. (3)
4. A soccer player takes a penalty
kick towards the goal. The angle at which the ball leaves
his/her boot
is 53 with respect to the ground. The penalty spot is 30 ft from the goal and
the
cross bar is 8 ft high (g = 32 ft/s2, tan(53) = 4/3).
(a) If the
ball hits the cross bar (i.e. it is exactly 8 ft high after traveling 30 ft),
how long does it
take to
reach the bar ? (9)
(b) What must be the initial velocity of the ball, vi ? (6)
(c) Determine
the horizontal and vertical components of the velocity of the ball upon impact
with the
cross bar. (6)
(d) Sketch
these velocity components and determine the tangent of the angle the velocity
vector
makes
with the vertical at the cross bar. (4)
5. A 50 kg crate is dragged across a floor by pulling on a rope inclined 370 above the horizontal. (g = 10 m/s2, cos(37) = 4/5)
(a) If the
coefficient of static friction is (1/3), what minimum tension in the rope is
required to
start
the crate moving ?
(12)
(b) If the
kinetic coefficient of friction is (1/4), what is the magnitude of the initial
acceleration
of the
crate ?
(13)