Physics 298

Sample Test 3

1)          A traveling wave on a string is described by,

   
    (a)     In which direction is this wave moving ?                                                            (2)

    (b)    What is the amplitude of the wave ?                                                                    (2)

    (c)    What is the wavelength of the wave ?                                                                  (3)

    (d)    What is the frequency of the wave ?                                                                    (3)

    (e)    What is the velocity of the wave ?                                                                       (3)

    (f)    If 1 metre of the string weighs 2 N, calculate the tension the string must be under to sustain
            the wave. (g = 10 m/s2).                                                                                        (6)

    (g)   What is the maximum speed of a particle on the string ?                                    (6)

Solution

2)  (a)    Two 85 g ice cubes are dropped into 30 g of water in a glass.  If the water is initially at a temperature of 50 C and if the ice comes directly from  the freezer at -300 C, what will be temperature of the drink when the ice and the water reach thermal equilibrium ?  How much ice and how much water are present at thermal equilibrium ?  Ignore the heat capacity of the glass and heat transferred to and from the environment.  For full credit carefully explain each step of your analysis.                                                   (13)

       (b)    Suppose that only one ice cube had been used in part (a), what would be the final temperature of the drink ?   How much ice and how much water are present at thermal equilibrium ?  Ignore the heat capacity of the glass and heat transferred to and from the environment.                  (12)

Solution

3)         A single pane of glass 1 cm thick, 50 cm wide and 100 cm long, loses heat from the inside
            of a house at a rate of 1.25 kW, when the inside of the house is maintained at 68F and the
            outside temperature is 23F.

    (a)    Calculate the thermal conductivity of the glass                                                 (5)

    (b)    The thermal conductivity of air is 40 times smaller than that of glass. The window pane is
             replaced by a double-glazed pane having a 1 mm air gap, indicated below. What are the
             temperatures of the inner faces of the glass (T1, T2) ?                                     (10)

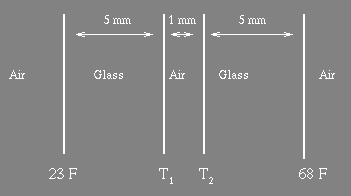
    (c)    Determine the rate of heat loss through this, double-glazed, window.            (6)

    (d)    In practice a double-glazed window is never able to achieve the reduction in heat loss
            determined from (a) to (c) above. Can you explain why this is the case ?        (4)

Solution

4)         At constant temperature, an ideal gas obeys Boyle's Law: PV = K, where K is a constant. A
            certain mass of ideal gas has a pressure of 150 kPa when its volume is 20 litres. (1 litre =
            10-3 m3).

    (a)    Determine the value of the constant K.                                                             (4)

    (b)    The gas undergoes an isothermal expansion, as indicated below, a to b. How much work is
             done by the gas during this expansion ? [ln(1.5) = 0.4]                                    (8)

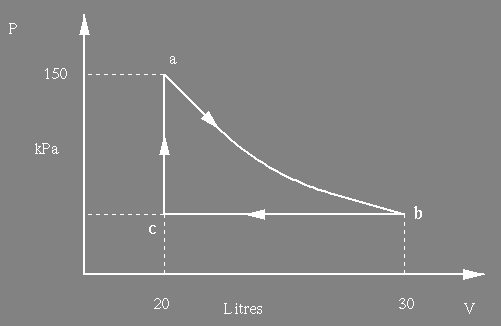
    (c)     If Ua = 30 J, assuming no change of state from a to b, what is Ub, and why ? (2)

    (d)    How much heat enters or leaves the system during the process a to b, and why ? (3)

    (e)    1000 J of work are done on the gas to take it from b to a via c. What is the pressure of the
             gas at c ?                                                                                                             (4)

    (f)    How much work is done by the gas during the complete cycle abca ?             (4)

Solution

5)        A 1 gram block oscillates back and forth along a straight line on a frictionless horizontal surface. It's displacement from the origin is given by,

       x = 5 (mm) cos[100π(rad/s)t + π/4(rad)]

(a)    What is the oscillation frequency ?        (4)

(b)    What is the maximum speed acquired by the block ? At what value of x does this occur ?    (7)

(c)    What is the maximum acceleration of the block ? At what value of x does this occur ?    (7)

(d)    What force, applied to the block, results in the given oscillations ?    (7)

Solution