Physics 298
Sample Test 2
1) A
missile, mass (2/9) kg, is projected at an angle of 670 with the
surface of the earth (assumed
horizontal), with a speed
of 65 m/s.
(a) What is the horizontal component of the missile's velocity when it reaches its maximum
height ? Ignore air resistance. (tan67 = 12/5) (3)
(b) Use conservation of energy to determine the maximum height reached by the missile. Ignore
air resistance. (g = 10 m/s2) (6)
(c) When
it reaches its maximum height the missile explodes, breaking into two equal
mass
fragments.
One fragment is observed to move horizontally, to the left (see above), with a
velocity
equal to twice that of the horizontal component of the original missile
immediately
before the explosion. Determine the velocity of the other
fragment immediately following
the
explosion. (8)
(d) How much kinetic energy is lost (or gained) in the explosion ? (6)
(e) Would you classify the explosion as elastic or inelastic ? (2)
2) When
suspended from a bungee cord, at rest, a 70 kg person - the "BUNGER"
- increases the
length of a 50 m cord by 25%.
(a) Assuming the cord obeys Hooke's Law, calculate its spring constant. (g = 10 m/s) (5)
(b) Use
the principle of energy conservation to determine how far the "BUNGER"
will fall when
jumping
from a bridge. (Ignore air resistance) (11)
(c) Assuming
zero air resistance how far would you expect the "BUNGER" to bounce
back
towards
the bridge ? (2)
(d) In a real situation, on the first bounce, the "BUNGER" returns to 10 m below the bridge.
How
much work is done against the resistive forces from the time the jump begins
till the top
of
this first bounce ? (7)
3) A soccer ball of mass 1kg is moving at a speed of 8 m/s.
(a) What is the magnitude of the momentum of the ball ? (4)
(b) What
is the kinetic energy of the ball ? (4)
(c) The ball strikes a brick wall and rebounds with a
speed of 5 m/s. Calculate the change in
momentum of the
ball. (6)
(d) If the ball is in contact with the wall for 0.1 s, what
is the magnitude of the force exerted
by the ball on the wall
? (6)
(e) The wall remains at rest relative to the earth. Is
the momentum of the system comprising
the
wall and the ball conserved ? If not, why not ? (5)
4) The
flywheel of a steam engine runs with a constant angular speed of 72 rev/min.
When the
steam
is shut off, the friction of the bearings and the air brings the wheel to rest
in 2 minutes.
(a) What is the constant angular acceleration, in rev/s, of the wheel during slowdown ? (7)
(b) How many rotations does the wheel make before coming to rest ? (7)
(c) What
is the tangential component of the linear acceleration of a particle that is 10
cm from
the
axis of rotation when the flywheel is turning at 6/(Ö(2p)) rev/mi (4)
(d) What is the magnitude of the net linear acceleration of the particle in (c) ? (7)
5) The
moment of inertia of a disc about an axis through its centre, perpendicular to
its plane, is
given
by (MR2)/2, where R is the radius and M the mass.
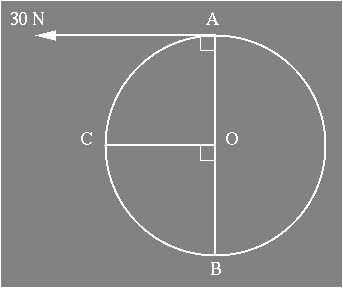
(a) Use
the parallel axis theorem to obtain an expression for the moment of inertia of
the disc,
about
an axis perpendicular to its plane, through its edge (at B). (5)
(b) A
force of 30 N is applied at point A, as shown above. If the disc has a radius
of 8 m,
determine the magnitude of the torque due to this force, abut the axis through B. (4)
(c) What
angular acceleration does this force impart to the disc, when it rotates about
the axis
through
B ? (M = 2.5 kg) (4)
(d) The
disk is rotating at 7 rev/min (about B), when a mass of 2.5 kg is placed on its
rim, at C.
What
is the angular velocity (in rev/min) of the disc (and the mass), immediately
after the
mass is positioned on it ? (8)
(e) What is the (linear) speed of the mass at this time ? (4)